Cálculo de colisiones entre objetos en un sistema tridimensional

En este artículo voy a explicar cómo he conseguido hacer que el personaje del juego se deslice por los objetos que encuentra a su paso. Para ello primero voy a exponer cómo resolverlo en un sistema bidimensional muy simple. Posteriormente cómo hacerlo en un sistema 2D más complejo. Y por último cómo aplicarlo a un sistema 3D.

En un sistema 2D simple

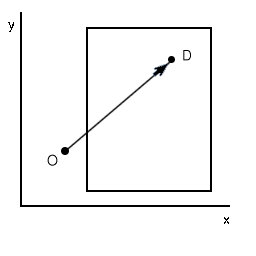Supongamos que estamos en uns sistema en 2D, como en un juego de plataformas. Imaginemos que los objetos de nuestro juego tienen forma de rectángulos y estos tienen los lados paralelos a los ejes de coordenadas. Supongamos que nuestro personaje se encuentra en el punto O y lleva cierta velocidad de modo que si nada nos lo impide en el siguiente turno se encontrará en D. Pero, sin embargo, nos topamos con un obstáculo. Para saber si un punto está dentro del rectángulo sólo tenemos que realizar una sencilla operación lógica. Si denominamos a P(x, y) a la esquina inferior izquierda del rectángulo de anchura 'a' y altura 'b'; y queremos saber si R(x', y') se encuentra dentro de este rectángulo, lo sabremos si:
(x' > x && x' < x+a && y' > y && y' < y+b).

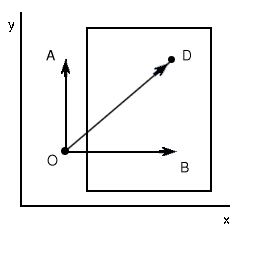Ahora que ya sabemos que no podemos movernos al punto D nuestro propósito es calcular la posición en el próximo turno una vez nos hallamos deslizado por el obstáculo que nos impide el paso. Pues bien, para ello calculamos los puntos A y B. A tiene como coordenada 'x' la coordenada 'x' de O; y como coordenada 'y' posee la coordenada 'y' de D. B tiene como coordenada 'x' la coordenada 'x' de D; y como coordenada 'y' posee la coordenada 'y' de O. Una vez tenemos estos dos puntos nos hemos de quedar con uno de ellos que será nuestro punto de destino en el próximo turno. Para ello calculamos cuál se encuentra fuera del rectángulo y nos quedamos con él. En este caso A será nuestro punto de destino.

Sistema 2D complejo

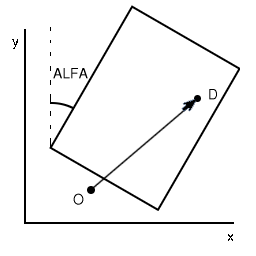  Pero trabajar con rectángulos que sólo se pueden colocar con los lados paralelos a los ejes de coordenadas puede resultar muy aburrido. Bien, imaginemos que en nuestro mundo ya tenemos rectángulos situados de múltiples formas diferentes. Ahora veamos en qué afecta esto a los cálculos que debemos realizar para calcular nuestro punto de destino.

Supongamos que nuestro personaje está en el punto O y, como en el caso anterior lleva cierta velocidad, de modo que si nada se lo impide en el siguiente turno se situará en el punto D. En el caso anterior la forma para saber si un punto estaba dentro de un rectángulo era muy sencilla puesto que todos los objetos se situaban con sus lados paralelos a los ejes de coordenadas; sin embargo ahora no nos es tan fácil realizar este cálculo. Para saber si el punto D está dentro de alguno de los objetos que existen en nuestro juego deberemos recorrer la lista/vector/array en la que guardemos los datos de los objetos y realizar los siguientes cálculos. Lo primero que tenemos que hacer es crearnos un sistema cartesiano con origen en O. Ahora calculamos las coordenadas de D y de P respecto de este sistema cartesiano, siendo P el punto de 'origen' del rectángulo (su esquina inferior izquierda). Esto se consigue simplemente restando a cada punto las coordenadas de O respecto del sistema cartesiano original. Ahora debemos girar nuestro sistema cartesiano un ángulo -ALFA, siendo ALFA el ángulo que necesita girar el rectángulo para ponerse con los lados paralelos a los ejes de coordenadas. El ángulo a girar el sistema cartesiano es -ALFA, ya que lo giramos en el sentido de las agujas del reloj que es el sentido negativo de medición de ángulos. Sin embargo, girar un sistema cartesiano un ángulo -ALFA es equivalente a girar todos los puntos contenidos en él un ángulo ALFA. Para que se entienda pongo un ejemplo: si giras la cabeza hacia la izquierda ves lo mismo que si todos los objetos se movieran hacia la derecha. Por lo tanto tenemos que girar los puntos D y P un ángulo ALFA. Para ello usamos esta formulita de fácil deducción para el que sepa trigonometría:

x' = x*cos(ALFA)-y*sen(ALFA)
y' = x*sen(ALFA)+y*cos(ALFA)

[x' e y' son las coordenadas resultantes de girar el punto (x, y) un cierto ángulo ALFA.]

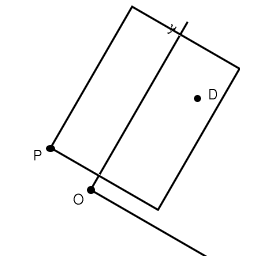
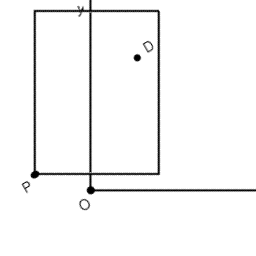
Sistema cartesiano una vez girado con origen en el punto O.	El mismo sistema cartesiano puesto derecho conforme nuestra visión

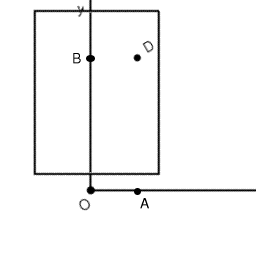Como veis ya tenemos el rectángulo listo para saber si nuestro punto de destino se encuentra dentro de él. En el caso de que el punto se encuentre dentro del rectángulo deberemos proceder como en el caso anterior. Calculamos los puntos A y B, y elegimos el que se encuentre fuera del rectángulo. Para calcular A y B simplemente tenemos que sumar a las coordenadas de O, la coordenada 'x' de D (para A), o la coordenada 'y' de D (para B). En nuestro caso nos quedamos con A, que es el que se encuentra fuera del rectángulo. El problema que tenemos es que tenemos las coordenadas del punto de destino, B, respecto de nuestro sistema cartesiano y necesitamos calcularlas respecto del sistema cartesiano original. Para calcularlas realizamos el proceso inverso, es decir, giramos el punto un ángulo (-ALFA) y sumamos al punto resultante las coordenadas de O.

x' = x*cos(-ALFA)-y*sen(-ALFA) + x0
y' = x*sen(-ALFA)+y*cos(-ALFA) + y0

  [x' e y' son las coordenadas resultantes de girar el punto (x, y) un cierto ángulo -ALFA y sumarle las coordenadas de O(x0, y0).]

Aquí se puede observar cuál será el punto final del movimiento. Se aprecia facilmente que la longitud recorrida será sensiblemente menor ya que el personaje va muy perpendicularmente al objeto.

Sistema 3D

Hasta aquí el asunto es relativamente sencillo, sin embargo, debemos trasladar estos conceptos a un sistema tridimensional y los cálculos se multiplican por 3, ya que giraremos en tres ejes diferentes.

Bien en principio todo es igual pero con una coordenada más. Primero nos creamos nuestro sistema cartesiano (primero sin girarlo) con origen en el punto de origen del desplazamiento que llamaremos O. Calculamos las coordenadas de D (punto de destino) y de P (origen del prisma del cual queremos saber si contiene al punto D) respecto de este nuevo sistema cartesiano. Para ello simplemente tenemos que restar a cada uno de los puntos las coordenadas de O. Ahora es cuando tenemos que comenzar a rotar. En un mundo 3D los objetos pueden estar girados en tres ejes diferentes por lo que, como ya he dicho, nuestras operaciones se multiplican por 3. El orden en el que vayamos girando los ejes no interviene en el resultado final. Por elegir alguno, comenzaremos girando las coordenadas de los puntos respecto del eje x. Para calcular estas coordenadas la fórmula es similar:

z' = z*cos(angulox)-y*sen(angulox)
y' = y*cos(angulox)+z*sen(angulox)

Podemos cometer el error de cambiar las 'z's por las 'y's, pero de acuerdo al sentido positivo de giro este es el orden de correcto.

Para girar en el eje y usamos esta fórmula:

x' = x*cos(anguloy)-z*sen(anguloy)
z' = z*cos(anguloy)+x*cos(anguloy)

Y por último para girar en el eje z usamos esta:

y' = y*cos(anguloz)-x*sen(anguloz)
x' = x*cos(anguloz)+y*sen(anguloz)

Estos cálculos debemos hacerlos con el punto D y con el punto P. Ahora ya tenemos el prisma con las caras y aristas paralelas al sistema cartesiano que nos hemos creado, de modo que nos resulta muy fácil saber si el punto D se encuentra dentro del prisma. Siendo 'a' la anchura del primsa, 'b' su altura, 'c' su profundidad y P(x0, y0, z0) el punto de origen del prisma, el punto D(x, y, z) se encontrará dentro de dicho primsa si:

x > x0 && x < x0+a && y > y0 && y < y0+b && z > z0 && z < z0+c

Cuando tratabamos el asunto en 2 dimensiones llegados a este punto si el punto se encontraba dentro del objeto debíamos calcular 2 puntos y elegir uno de los dos. Pues bien, en tres dimensiones no tenemos 2 puntos sino 6 puntos (una vez más se nos multiplica el trabajo por 3). Si las coordenadas del punto de destino, D, con respecto a nuestro sistema cartesiano son (x, y, z) deberemos ir probando puntos de esta forma:

(x, y, 0)
(0, y, z)
(x, 0, z)
(x, 0, 0)
(0, y, 0)
(0, 0, z)

El orden no importa siempre y cuando primero probemos primero con los puntos que contienen dos coordenadas del punto D, ya que así el cálculo se hará de forma correcta. Una vez hallamos encotrado que uno de los puntos está fuera del prisma, calcularemos sus coordenadas respecto del sistema cartesiano original. Esto se consigue haciendo los cálculos inversamente. Primero realizaremos los giros de igual modo pero con los ángulos: -angulox, -anguloy, -anguloz. Es decir giraremos en sentido negativo. Una vez hecho esto simplemente nos queda sumarle las coordenadas del punto O, y ya tenemos nuestro punto de destino.

Observaciones para la implementación del algoritmo:

Primero voy a exponer algunos errores que cometí al implementar este algoritmo para que sirva para que nadie más caiga en ellos:

Un error que cometí fue usar sólo tres variables al realizar los giros de ejes. Si por ejemplo tenía las variables (x, y, z) con las coordenadas de un punto y a continuación lo quería girar hice esto:

x = x*cos(angulo)-z*sen(angulo)
z = z*cos(angulo)+x*cos(angulo)

en seguida me dí cuenta que en realidad en la segunda línea estaba usando la coordenada x una vez girada, y no la coordenada x original (sin girar) que se debe usar. Por ello se deben usar unas variables auxiliares que conserven los valores de las coordenadas entre giros.

Otro error es el siguiente:

Para calcular si el punto destino se encuentra dentro de algún objeto recorremos los objetos que forman parte del juego. Una vez encontrado un objeto que contenga nuestro punto de destino calculamos las coordenadas del punto si nos deslizáramos por dicho objeto y salimos del bucle. Al hacer esto no contamos con la posibilidad de que más de un objeto contenga nuestro punto de destino por lo que si por ejemplo nos vamos a una esquina nos encontramos con que nos estamos deslizando correctamente por una pared pero que la otra la atravesamos sin problemas. Por ello debemos volver a recorrer la lista de objetos con las nuevas coordenadas del punto de destino. Sin embargo hay que tener cuidado porque en ciertas ocasiones esto puede provocar un bucle infinito. Esto lo he solucionado con una variable contador que en caso de llegar a un valor límite (que he establecido en numero_objetos²) detiene el bucle y pone como coordenadas de destino las de origen, es decir no nos movemos. Esto que puede parecer una chapuza (quizá lo es) no se nota en el juego.

Ahora expongo algunas soluciones para hacer más rápido el código:

Es obvio que las funciones seno y coseno son muy usadas, y en el código son usadas hasta cuatro veces con el mismo argumento, por lo que es muy apropiado crearse un par de variables auxiliares que almacenen los valores calculados para usarlos en el resto de ocasiones.

A veces un objeto está tan alejado del punto de destino que es imposible que lo contenga por muchos giros que efectue. Esto ocurrirá cuando la distancia del punto de destino al punto de origen del prisma sea mayor que la diagonal del prisma. Para calcular la diagonal del prisma debemos hallar el módulo de un vector de componenetes (a, b, c) siendo estas su anchura, altura y profundidad respectivamente. Esto se hace de la siguiente manera:

modulo = (a*a + b*b + c*c)¹/2

Es decir, el módulo es la raiz cuadrada de la suma de los cuadrados de las componentes del vector. Sin embargo calcular una raiz cuadrada consume más recursos que hacer todos los giros de ejes. No obstante lo que buscamos es un número que sea lo más aproximado a la diagonal del prisma pero que sea mayor que ella; no buscamos un número exacto sino una estimación. Sin ningún problema podríamos descartar todos aquellos objetos que se encontraran a mayor distancia del punto de destino que a+b+c. Para demostrar que a+b+c es mayor que la diagonal del primsa os invito a imaginar un triángulo rectángulo. En él la hipotenusa siempre es menor que la suma de sus catetos.

Bueno hasta aquí todo.

Si has llegado hasta aquí, gracias y espero que te haya sido útil.