Complexity and evolutionary simulation models in cognitive science
Epistemology of synthetic bottom-up simulation modelling

Xabier Barandiaran1
xabier@barandiaran.net
http://barandiaran.net

26-06-03

Abstract

In complex adaptive systems, where internal and external non-linear interactions give rise to an emergent functionality, analytic decomposition of component and isolated functional evaluation of them is not a viable methodological practice. More recently, embodied bottom-up synthetic methodological approaches have been proposed to solve this problem. Evolutionary simulation modelling (specifically evolutionary robotics) provides an explicit research methodology in this direction. We argue and illustrate that the scientific relevance of such methodology can be best understood in terms of a double conceptual blending: i) a conceptual blending between structural and functional levels of description embedded in the simulation; and ii) a methodological blending between empirical and theoretical work in scientific research. Simulation models show their scientific value on: reconceptualization of theoretical assumptions; hypothesis generation and proof of concept. We conclude that simulation models are capable of extending our cognitive and epistemological resources to (re)conceptualise scientific domains and to establish causal relations between different levels of description.

Keywords

Scientific methodology, cognitive science, models, artificial life, simulation of adaptive behaviour, emergence, epistemology, explanation, conceptual blending, metaphors in science

Copyleft

Complexity and evolutionary simulation models in cognitive science. Epistemology of synthetic bottom-up simulation modelling. v.1.0

Copyright © 2003 Xabier Barandiaran.
Copyleft  2003 Xabier Barandiaran:

The licensor permits others to copy, distribute, display, and perform the work. In return, licensees must give the original author credit. The licensor permits others to copy, distribute, display, and perform the work. In return, licensees may not use the work for commercial purposes --unless they get the licensor's permission. The licensor permits others to distribute derivative works only under a license identical to the one that governs the licensor's work.

This is not mean to be the full license but short guide of it. The full license can be found at:

http://creativecommons.org/licenses/by-nc-sa/1.0/legalcode

Versions

v.1.0  26-06-03   

Formats and Sources

html http://sindominio.net/~xabier/textos/blending/blending.html
pdf http://sindominio.net/~xabier/textos/blending/blending.pdf
ps http://sindominio.net/~xabier/textos/blending/blending.ps
sources http://sindominio.net/~xabier/textos/blending/

Cite

Xabier Barandiaran (2003) Complexity and evolutionary simulation models in cognitive science. Epistemology of synthetic bottom-up simulation modelling. v.1.0. url:
http://sindominio.net/~xabier/textos/blending/blending.pdf


Contents

1 Structure and function: limits of traditional mechanistic methodology in complex systems

1.1 Complexity and localisation

The Cartesian method of divide and conqueer, the decomposition of a system in components and their isolated analysis has long been the mainstream methodological strategy of scientific enquiry on the understanding of functional systems, i.e. mechanistic explanations.

In the field of cognitive science computational functionalism has proceed by what Bechtel and Richardson (1993) call a synthetic top-down decompositional method, i.e. decomposing functional or task related cognitive structures (perception, memory, reasoning, action, etc.) dividing them into sub-components, and establishing a set of computational relations among subsystems.

On the other hand neuroscientific research has focused on neurophysiological decomposition of neural structures and localisation of such functional cognitive components: an analytic bottom-up approach.

We shall understand localisation (the main mechanistic explanatory strategy) as a mapping between a physical structure (operationally tractable set of variables, whether they are biochemical or neurodynamic) and a functional structure (a set of computational components). Advances on neurophysiology and computational functionalism shall, in turn, end up providing us with such mechanistic explanation if: a) we don't want to assume a metaphysical dualism, and b) computational-functionalist interpretations of cognitive behaviour are to be considered the `right' functional interpretation among all the possible ones.

The problem arises when recent interest on complex systems has shown that such methodology (decomposition and localisation) fails to understand nonlinear systems Langton (1996). When the interactions between components are non-linear the principle of aggregation or localisation presupposed in traditional decompositional methods does not hold. The system is more than the sum of its parts, the superposition of isolated components does not give rise to the essential properties of the whole system. It is the non-linear interaction between components what determines the properties of the system creating a kind of structural complexity where the relation between function and structure cannot be established by the traditional decompositional method; i.e. no mapping can be established between functional components and structural (neurophysiological) components.

In addition to this structural complexity we have an interactive complexity where the system interacts with its environment in such a way that the overall functionality of the system emerges from highly interactive loops. But things can go even worst on complexity, as Harvey et al. (1997) put it: ``Interactions between separate sub-systems are not limited to directly visible connecting links between them, but also include interactions mediated via the environment'' (p.205).

As Clark (1996,1997) has pointed out the nature of what he calls interactive emergence seriously compromises the classical computationalist definition of function by:

Thus in complex adaptive systems where internal and external nonlinear interactions give rise to an emergent functionality top-down functional or task decomposition and their structural localisation is not a viable methodological practice. In mathematical terms structural complexity is a consequence of the impossibility of the analytic solution for the nonlinear differential equations determining system behaviour and the high sensitivity of the system to boundary conditions (when it exploit particular features of the environment to achieve functionality) or the opposite, the metaestability of the system under structural perturbations, i.e. its self-regulating capacity.

1.2 Complexity in cognitive science

In the realm of cognitive science both aspects of emergent functionality (the structural and interactive) gave rise to two different radical modification of the orthodox functionalist-computationalist research program (Block, 1996; Fodor, 1987). Concerning structural emergence the PDP approach showed that cognitive processing was not the output of sequential symbol manipulation procedures but the outcome of highly distributed sub-symbolic networks. The interactive complexity has been highlighted by the more recent embodied and situated approach to cognition (Brooks, 1991b,a; Pfeifer and Scheier, 1999).

What embodiment and situatedness illustrates is that the way the specific adaptive function is achieved involves a dynamic coupling between agent and environment where no structure of the agent can be pointed to be sufficient for the function to happen. We can contrast this embodied and situated functionality, what Luc Steels has called emergent functionality (Steels, 1991), as opposed to hierarchical systems. Hierarchical systems are those where the system can be decomposed into different components which perform isolated functions by directly controlling the variables defining the function, i.e. the structure of the mechanism and the function it performs are codefined, localisation is possible. An example of a hierarchical system is a motor engine where, for example, a valve that controls the flow of oil to an engine performs it function by directly manipulating the size of the gap through which the oil flows.

Bonabeau and Theraulaz (1995) show how the manipulation of boundary conditions2not defining the function itself play a fundamental role in the performance of emergent functions. Given an environment $E=\{x_{1}, x_{2}, \ldots, x_{n}, \ldots, x_{m}\}$ and the subset of environmental variables defining a function $E_{n}= \{x_{1}, x_{2}, \ldots, x_{n}\}$ a function is defined as $F(E_{n}) = dx_{1}/dt, \ldots, dx_{n}/dt$. An structure $S$ performs the function F iff: $S(E)=F(E_{n})$. What reductionists3 presuppose is that $\{x_{n+1}, \ldots, x_{m}\}$ remains constant, i.e. $\delta S / \delta x_{i} = 0 $ for $i= \{n+1, \ldots, m\}$. In short: reductionists believe that the external variables of those defining a function do not affect how a structure performs that function. Embodiment and situatedness shows how agents exploit many features of their body and environment (boundary conditions) to perform functions which are not defined by those body/environment features. In other words localisation (i.e. mapping between structural and functional components) cannot succeed because the system exploits interactive feed-back loops with environmental features to satisfy functionality.

The way some adaptive systems exploit several environmental features to perform functions and the highly interconnected and recursive nature of the causal network of their internal structure does not allow for the traditional analytic methods to be successfully aplied. Under this situation new methodologies has been proposed as suitable tools to explore complex systems: what we will call synthetic bottom-up simulation modelling.

2 Synthetic bottom-up simulation modelling

2.1 The situated, synthetic bottom-up approach

During the late 80s and early 90s a new methodological paradigm for the study of complex adaptive systems came to being. Alife (Bedau, 2001; Langton, 1996) and situated robotics proposed a bottom-up, situated and synthetic approach toward the modelling of complex systems.

The approach is synthetic because understanding of a systems is expected to be achieved by building similar systems; i.e. by synthesis rather than analysis. The approach is bottom-up because the functionality of the system is achieved as emergent from structural local rules and local system environment interactions rather than functional components and informational input-output relations between them. Repeated and distributed local interactions give rise to a global pattern of system behaviour, it is in this global pattern that functionality is found and not in the local components of the system; i.e. there is no mapping between structural components and functional components. There is no explicit encoding of the global behaviour. Finally the approach is situated: systems are built in real or simulated environments with direct sensory-motor links (i.e. input-output relationships are not symbol based). This methodology is the core of Alife techniques (Bonabeau and Theraulaz, 1995; Bedau, 2001; Langton, 1996) and embodied and situated robotics (Brooks, 1991b,a; Pfeifer and Scheier, 1999), among others. In order to understand the scientific value of such methodology we shall focus on a well established and successful specific methodology which is that of evolutionary robotics (Nolfi and Floreano, 2000; Harvey et al., 1997; Husbands et al., 1997) and Randall Beer's minimally cognitive behaviour program (Slocum et al., 2000; Beer, 2001).

2.2 Evolutionary Robotics and the minimally cognitive behaviour program

Since structural decomposition of a complex system fails to grasp the essential local interactions that give rise to functional behaviour synthesis looks like a natural way to deal with such a problem, it is on the synthesis that knowledge is achieved, on the manipulation of parameters and local rules while putting together the components of the system. But the very nature of complex systems makes its synthesis a problematic issue, that's precisely the locus of complexity and, unlike functionalist top-down synthesis, complex systems are not manageable for human understanding4. As a solution to this problem artificial evolution has been widely used to synthetize a functional system. A particular case of this technique is given by evolutionary robotics and the minimally cognitive behaviour program.

Evolutionary robotics and evolutionary simulation models have successfully been applied to achieve a number of complex behaviours, among them: plastic development (Floreano and Urzelai, 2000,2001), robot team coordination and role allocation (Quinn et al., 2002), communication (Quinn, 2001), shape recognition (Cliff et al., 1993) , pursuit and evasion (Cliff and Miller, 1995), acoustic coordination (Di Paolo, 2000a), learning (Tuci et al., 2002), adaptation to sensory inversion and other sensorimotor disruptions (Di Paolo, 2000b), active categorical perception (Beer, 2001), short-term memory, self-nonself discrimination, selective attention, attention switching, anticipation of object movement (Slocum et al., 2000; Gallagher and Beer, 1999; Beer, 1996), etc...

Evolutionary simulation model synthesis proceeds as follows:

  1. Definition of a set of body, environment and neural structures (unspecified on their parameter values).
  2. Artificial evolution of parameters according to a given fitness function.
  3. Reproduction/simulation of system behaviour with numerical methods.

Body and environment can be real or simulated, in the last case khepera like robots are usually simulated (i.e. circular two dimensional robots with two wheels and different sensors) and the resulting controll architecture exported to the real robot (not without problems (Jakobi et al., 1995)). What is interesting for our discussion is the structure of the neural controll architecture. The basic structure of the neural network is generally a Continuous Time Recurrent Neural Network CTRNN (which are in principle capable of the dynamical behaviour of any other dynamical system with a finite number of variables (Funakashi and Nakamura, 1993)). CTRNNs are fully connected, recursive, dynamic (time and rate dependant), controll architectures specified by the following state equation:


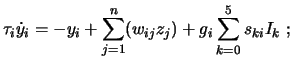$\displaystyle \tau_{i} \dot{y}_{i} = -y_{i} + \sum_{j=1}^n(w_{ij}z_{j}) + g_{i}\sum_{k=0}^{5} s_{ki}I_{k}~;$      
$\displaystyle \textrm{where}~~~z_{j} = \frac{1}{1+exp(-(y_{j}+b_{j}))}$     (1)

where $y$ is the state of each neuron, $\tau_{i}$ is the time constant (decay constant for neural activity), $w_{ij}$ is the connection weight between neuron $i$ and $j$, $z_{j}$ is the activation of neuron $j$, $y_{j}$ is $j$'s state and $b_{j}$ a bias term; $g_{i}$ is a gain applied to the overall sensory input to the neuron, $s_{ki}$ is the input weight from sensor $k$ to neuron $i$ and $I_{k}$ is the input value of sensor $k$. States are initialized at 0 or a random value and the CTRNN is integrated using forward Euler method. All neurons are connected to each other and to themselves.

Over this basic architecture more complex mechanisms can be implemented, such as gas-nets (Husbands et al., 1998) and synaptic plasticity (Floreano and Urzelai, 2001; Di Paolo, 2000b).

Controll parameters (plastic rules, time constants, number of neurons, weight values, etc...) are left to evolutionary search as well as some body-sensor parameters (motor transfer parameters, position of sensors, etc. -depending on the particular case). The structure of the simulation is thus defined as a dynamical system and is implemented in a simulation model where the state of the system is numerically calculated for short time-steps.

After deciding the basic structure of the simulation a genetic algorithm is used to evolve the parameters with the following procedure:

  1. All the parameters are encoded in a genotype (taking random values constrained between pre-specified values).
  2. A population of genotypes is randomly created.
  3. A fitness function is defined to asses the fitness of the produced behaviour given a set of parameter values (genotype). Examples of fitness function are distance to a given object, performance in a learning task, stability and robustness of walking behaviour, etc.
  4. All the genotypes in the population are evaluated according to the fitness function in the body-environment simulation.
  5. The best genotypes are selected for reproduction and a new population (generation) of genotypes is created and randomly mutated.
  6. Steeps 4 and 5 are repeated until a given fitness value is achieved.

In brief what we get is a simulation model were local interaction rules (achieved determining parameter values through evolution), recursively (through the numerical calculation of states) applied give rise to a global system behaviour (specified by the evolutionary fitness function). The question now is how does this modelling technique contribute to scientific development once decomposition and localisation are shown to be unapropiate methods?

3 Methodological and conceptual blending

The role of bottom-up synthetic simulation models (and more specifically evolutionary robotic simulations) is, we will argue, that of providing: a) a conceptual blending between lower level mechanisms and global behavioural patterns and b) a methodological blending between empirical and theoretical domains. We take the notion of blending (and conceptual blending in particular) from Fauconnier and Turner (1998) who analyse conceptual blending as a major cognitive process in which projections from two different conceptual spaces blend into a single conceptual space on which new relations and structures are discovered, which feed-back to the input spaces thus producing new knowledge.

3.1 Simulations as conceptual blenders

The problem of functional decomposition explained above has been skipped in traditional scientific practices by dividing natural objects of study on different levels of description and finding specific observables on each level and lawfull regularities among those observables. This way neurophysiological and behavioural or cognitive levels of observation become two separated scientific domains. The problem arises when localisation of functional (cognitive) components into structural components fails as a result of the underlying complexity of the system.

In such cases we believe that simulation models act as computational and exteriorized conceptual blenders, where two distinct conceptual spaces, structural (neurodynamical) and behavioural (cognitive), merge into the simulation, feeding back to both input domains. Simulation models in evolutionary robotics are not neurobiological models (in fact they are generally very poor in comparison with computational neuroscientific models of neurons), nor they are purely cognitive models (which are often build in purely functional or representational terms) but conceptual blender between both functional and neurobiological models.

At a first view it could be argued that the blended space being artefactual doesn't satisfy Fauconnier and Turner's theory which presupposes that the blended space is a mental space and that cognitive operations on that mental space are the source of new knowledge. Nontheless, carefully analysed, simulation models do in fact satisfy most (if not all) of the characteristics of mental blending spaces. The neurophysiological input space projects into the blended through the abstraction of local rules from neurophysiological models. The cognitive input space projects by conceptualising the emergent behavioural pattern as non trivially cognitive; i.e. the emergent global behaviour is considered a cognitive behaviour. What remains opaque (until the experimenter abstracts explanatory patterns) is the cross-pace mapping, because of the dynamical complexity of the emergent phenomena. In the case of evolutionary robotics artificial evolution is used to create the blended space, and numerical calculations to run the blended space which is not purely relational but dynamical.

Figure: Simulation models in scientific processes
Image /home/xkrop/trabajos/blending//epist.png

The main difference between mental and artifactual blended spaces is not its position in relation to the skull (after all cognitive capacities are well understood as being distributed and also extracraneal Clark and Chalmers (1998)) but the capacity of computational simulation models to solve differential equations numerically and implement massive and recursive computations to produce emergent simulation models; human manipulation, transformation and experimentation with the computational model works as well as it does with mental models.

3.2 Simulations as methodological blenders

After deciding what evolutionary simulation models are the question now is to understand what is their scientific value if they aren't models of biological phenomena nor models of cognitive functionality; if they don't even try to fit any empirical data (Di Paolo et al., 2000).

We believe that simulation models are better understood as methodological blenders (this time in a loose sense of blending only metaphorically related to Fauconnier and Turner's work) between purely empírical and purely theoretical domains (whether this extreme positions exist or not, as such, is not an issue here). Specially significant is the relation simulation models establish between theoretical assumptions (adaptationism, representation, innateness, etc.) and empirical models.

Di Paolo et al. (2000) argue that simulation models work as opaque thought experiments halfway between empirical models (in virtue of their capacity to produce non-trivial data through the computational emergence of global patterns) and theoretical tools (since they address abstract theoretical/conceptual issues rather than specific empirical targets, unlike biorobotic models (Webb, 2001)). Following their argument we believe that simulation models show a scientific value on:

4 Conclusion

The scientific value of computational simulation models can be understood, from a higher perspective, as diminishing the constraints acting upon scientific development, as defined by Bechtel and Richardson (1993). In relation to psychological constraints it shall be clear by now that simulation models extend human capacities providing a kind of externalized and computationally powerfull conceptual space in silico. At the same time the way in which human understanding is constrained on big search spaces is now been solved by artificial evolution as a genuine tool to explore search spaces (Mitchell, 1996). Thus there are, at least, two ways in which human psychological capacities are enhanced with simulation models (other than the classical memory capacity, computational power, and speed): a) by conceiving dynamical objects composed of highly interacting components, and b) by exploring search spaces with artificial evolution. On the side of phenomenological constraints we believe that simulation models come to produce new artificial phenomena which can be studied (and often are) in their own right, and in a scientifically relevant way when considered as artifactual phenomena blending distinct modelling (scientific) spaces. It is possibly in relation to operational constraints where simulation models have being traditionally considered to have a major contribution, on that simulation models provide to the experimenter a complete control over variables, and repeatability under different conditions. Finally physicall constraints are considered by Bechtel and Richardson (1993) as limiting the range of allowed component functions by the requirement that they must be shown to depend systematically on physical structures. Once again we believe that evolutionary simulation models provide one of the most powerfull cognitive tools to explore the systematic dependencies between lower level mechanistic (physical) constraints and the produced emergent phenomena, acting themselves (when no other complexity reduction is possible --by extracting intermediate explanatory patterns) as explanations of bottom-up causation.

We conclude that simulation models are capable of extending our cognitive and epistemological resources to (re)conceptualise scientific domains and to establish causal relations between different levels of description. Simulation models become, blended with traditional empirical methodology, crucial tools for the scientific research on complex systems and cognitive science.

Bibliography

Bechtel, W. and Richardson, R. (1993).
Discovering Complexity. Decomposition and Localization as strategies in scientific research.
Princeton University Press.

Bedau, M. (2001).
Artificial Life.
In Floridi, L., editor, Blackwell Guide to the Philosophy of Computing and Information, page FALTA. Blackwell.

Beer, R. D. (1996).
Toward the evolution of dynamical neural networks for minimally cognitive behaviour.
In Maes, P., Mataric, M., Meyer, J. A., Pollack, J., and Wilson, S., editors, From Animals to Animats 4: Proceedings of the Fourth International Conference on Simulation of Adaptive Behaviour, pages 421-429. Harvard, MA: MIT Press.

Beer, R. D. (2001).
The dynamics of active categorical perception in an evolved model agent.
submitted to Behavioral and Brain Sciences.
Downloaded on 13/3/02 from http://vorlon.cwru.edu/~beer/.

Block, N. (1996).
What is Functionalism. Online revised entry on functionalism in the .
In Borchert, D., editor, The Encyclopedia of Philosophy Supplement. MacMillan.
URL:
http://www.nyu.edu/gsas/dept/philo/faculty/block.

Bonabeau, E. and Theraulaz, G. (1995).
Why do we need Artificial Life?
In Langton, C., editor, Artificial Life. An overview, pages 303-325. MIT, Cambridge, MA.

Brooks, R. A. (1991a).
Intelligence without reason.
In Proceedings of the 12th International Joint Conf. on Artificial Intelligence, pages 569-595.

Brooks, R. A. (1991b).
Intelligence without representation.
Artificial Intelligence Journal, 47:139-160.

Clark, A. (1996).
Happy couplings: Emergence and explanatory interlock.
In Boden, M., editor, The Philosophy of Artificial Life, pages 262-281. Oxford University Press.

Clark, A. (1997).
Being There: putting, body and world together again.
MIT, Cambridge, MA.

Clark, A. and Chalmers, D. (1998).
The Extended Mind.
Synthese, 101:401-431.

Cliff, D., Harvey, I., and Husbands, P. (1993).
Explorations in evolutionary robotics.
Adaptive Behavior, 2(1):71-104.

Cliff, D. and Miller, G. (1995).
Tracking the Red Queen: Measurements of adaptive progress in co-evolutionary simulations.
In Morán, F., Moreno, A., Merelo, J., and Chacón, P., editors, Advances in Artificial Life: Proceedings of the Third European Conference on Artificial Life, pages 200-218. Springer Verlag.

Di Paolo, E. (2000a).
Behavioral coordination, structural congruence and entrainment in a simulation of acoustically coupled agents.
Adaptive Behavior, 8(1):25-46.

Di Paolo, E. (2000b).
Homeostatic adaptation to inversion of the visual field and other sensorimotor disruptions.
In Meyer, J.-A., Berthoz, A., Floreano, D., Roitblat, H., and Wilson, S., editors, From Animals to Animats 6: Proceedings of the Sixth International Conference on Simulation of Adaptive Behavior, pages 440-449. Harvard, MA: MIT Press.

Di Paolo, E., Noble, J., and Bullock, S. (2000).
Simulation Models as Opaque Thought Experiments.
In Bedau, M., McCaskill, J., Packard, N., and Rasmussen, S., editors, Artificial Life VII: The 7th International Conference on the Simulaiton and Synthesis of of Living Systems. Reed College, Oregon, USA.

Fauconnier, G. and Turner, M. (1998).
Conceptual Integration Networks.
Cognitive Science, 22(2):133-187.

Floreano, D. and Urzelai, J. (2000).
Evolutionary robots with online self-organization and behavioural fitness.
Robotics and Autonomous Systems, 13:431-443.

Floreano, D. and Urzelai, J. (2001).
Neural Morphogenesis, Synaptic Plasticity, and Evolution.
Theory in Biosciences.

Fodor, J. (1987).
Psychosemantics.
Cambridge, MA: MIT Press.

Funakashi, K. and Nakamura, Y. (1993).
Approximation of dynamical systems by continuous time recurrent neural networks.
Neural Networks, 6:1-64.

Gallagher, J. and Beer, R. (1999).
Evolution and analysis of dynamical neural networks for agents integrating vision, locomotion, and short-term memory.
In Banzhaf, Daida, E. G. H. and Smith, editors, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-99), pages 1273-1280.

Harvey, I., Husbands, P., Cliff, D., Thompson, A., and Jakobi, N. (1997).
Evolutionary Robotics: the Sussex Approach.
Robotics and Autonomous Systems, 20:205-224.

Husbands, P., Harvey, I., Cliff, D., and Miller, G. (1997).
Artificial Evolution: A New Path for Artificial Intelligence?
Brain and Cognition, 34:130-159.

Husbands, P., Smith, T., Jakobi, N., and O'Shea, M. (1998).
Better living through chemistry: Evolving GasNets for robot control.
Connection Science, 10(3-4):185-210.

Jakobi, N., Husbands, P., and Harvey, I. (1995).
Noise and the reality gap: the use of simulation in evolutionary robotics.
In Morán, F., Moreno, A., Merelo, J., and Chacón, P., editors, Advances in Artificial Life: Proceedings of the Third European Conference on Artificial Life, pages 704-720. Springer Verlag.

Langton, C. (1996).
Artificial Life.
In Boden, M., editor, The Philosophy of Artificial Life, pages 39-94. Oxford University Press, Oxford.

Mitchell, M. (1996).
An introduction to genetic algorithms.
MIT Press, 1998 edition.

Nolfi, S. and Floreano, D. (2000).
Evolutionary Robotics: The Biology, Intelligence and Technology of Self-Organizing Machines.
MIT Press.

Pfeifer, R. and Scheier, C. (1999).
Understanding Intelligence.
MIT.

Quinn, M. (2001).
Evolving communication without dedicated communication channels.
In Kelemen, J. and Sosik, P., editors, Proceedings of ECAL01, pages 357-366. Springer Verlag.

Quinn, M., Smith, L., Mayley, G., and Husbands, P. (2002).
Evolving formation movement for a homogeneous multi-robot system: Teamwork and role allocation with real robots.
Cognitive Science research paper 515, University of Sussex, UK.

Slocum, A. C., Downey, D. C., and Beer, R. D. (2000).
Further experiments in the evolution of minimally cognitive behavior: From perceiving affordances to selective attention.
In Meyer, J., Berthoz, A., Floreano, D., Roitblat, H., and Wilson, S., editors, From Animals to Animats 6: Proceedings of the Fourth International Conference on Simulation of Adaptive Behavior, pages 430-439. Harvard, MA: MIT Press.

Steels, L. (1991).
Towards a Theory of Emergent Functionality.
In Meyer, J. and Wilson, R., editors, Simulation of Adaptive Behaviour, pages 451-461. MIT Press.

Tuci, E., Harvey, I., and Quinn, M. (2002).
Evolving integrated controllers for autonomous learning robots using dynamic neural networks.
In Proceedings of The Seventh International Conference on the Simulation of Adaptive Behaviour (SAB'02).

Webb, B. (2001).
Can robots make good models of biological behaviour?
Behavioural and Brain Sciences, 24:1033-1050.


Footnotes

... 1
The ideas developed in this paper have being originated in a paper working by Roberto Feltrero and myself. Complete authorship of the present paper shall recognize Roberto's contribution, specially on conceptual blending literature and fruitfull discussion on the topics involved.
... conditions2
According to Bonabeau and Theraulaz (1995) boundary conditions are those constraining lower-level processes to give rise to the ``proper'' emergent behavioural pattern. The internal local rules of a system (the neural network in an agent) are generally unspecific on their functionality. Extreme reductionism only considers internal explanations (logical/causal relationship defining functionality by means of their correspondence relation with the environmental variables defining the function) of the performance of a function.
... reductionists3
Bonabeau and Theraulaz take for reductionist those researches involved in the localisationist program
... understanding4
``Recent research in the psychology of judgement indicates that humans have great difficulty comprehending cases with more than a few interacting variables. Humans cannot use information involving large numbers of components or complex interactions of components, and even when the problem tasks are computationally tractable, human beings do not approach them in this way. Complex systems are computationally as well as psychologically unmanageable for humans'' (Bechtel and Richardson, 1993, p.27), emphasis on the original.

xkrop 2003-06-27